Entry Level mode
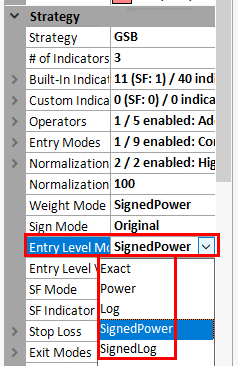
consider this
result = indicator1*indcator2*indicator3
If result > entrylevel and seondaryFilter=true then buy...
Indicators will range from -100 to 100 as they are normalized in this range.
Exact mode.
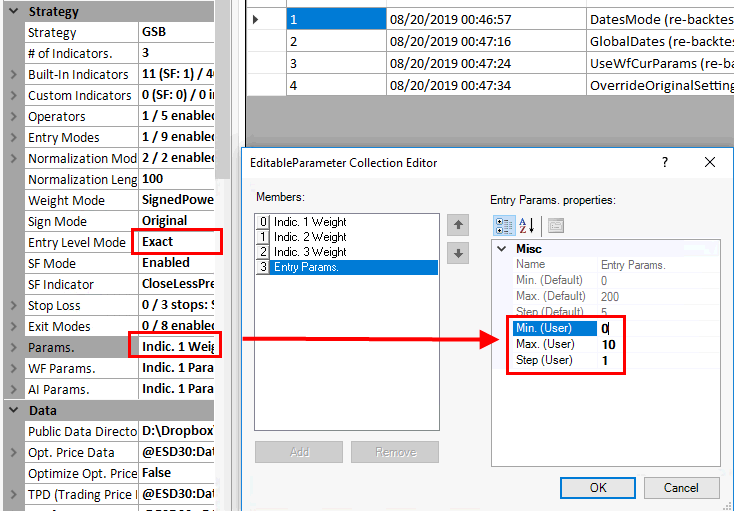
If EntryLevel exact is used, you could use entry level say 0 to 300 step 10 if we have the format below.
Weights 0 to 2 step 0.25
Result=indicator1*weight1+indicator2*weight2+indicator3*weight3
The highest possible value of result would be 100*2+100*2+100*2 = 300
If result{-300 to 300} > entrylevel {say entry Params 0 to 100 step 10} and seondaryFilter=true then buy...
So this will give a mild effect of making indicator results closer to zero not trade. This will give fewer trades
and possibly some immunity to noisy signals.
Power mode.
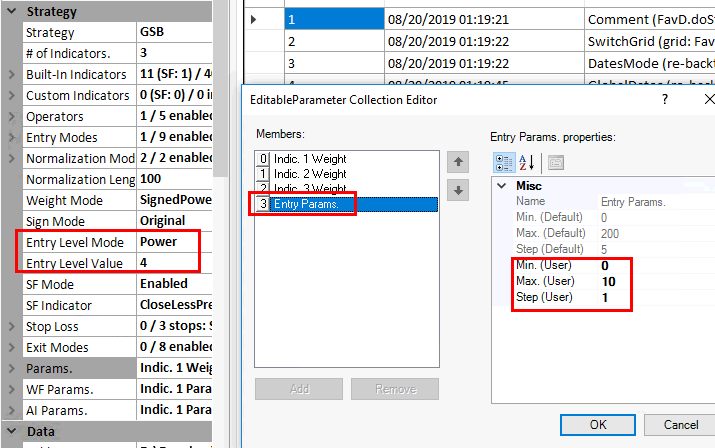
consider another example
result = indicator1*weight1*indcator2*weight2*indicator3*weight3
If result > entrylevel and seondaryFilter=true then buy...
The highest possible value of result would be 100*2*100*2*100*2= 8,000,000
So entrylevel of 0 to 300 would be way to low.
However entrylevel of 0 to say 1,000,000 step 10,000 is a bit coarse in its steps too.
This is why we have the power function. Power 4 is used in this example.
Entryparamaters 0 to 10 step 1 would give the values of
0 1 16, 81, 256, 625, 1296, 2401, 4096, 6561, 10000
This is considered more appropriate when we have a wide possible range of numbers in the result variable.
SignPower mode.
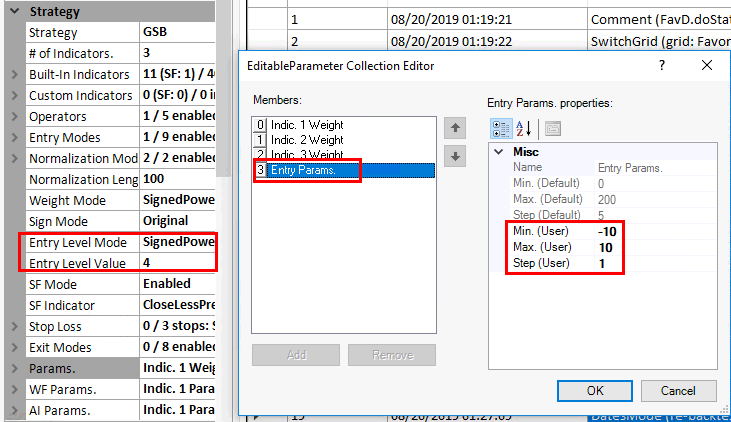
Signp(x) gives -1 for a number < 0, 0 for 0, and 1 for a number >0.
If we just used power mode, and used -10 to 10 our entry parameters would be
10000, 6561, 4096, 2401, 1296, 625, 256, 81, 16,1 0 1 16, 81, 256, 625, 1296, 2401, 4096, 6561, 10000
Sign power will in effect do the following when enty Parms are -10 to 10 step 1, entrylevel value ^4
Entrylevel=signp(parameters)*EntryParameters^entryLevelValue.
This would give entry level of
-10000, -6561, -4096, -2401, -1296, -625, -256, -81, -16,-1 0 1 16, 81, 256, 625, 1296, 2401, 4096, 6561, 10000